Question

A 10.0-cm-long wire is pulled along a U-shaped conducting rail in a perpendicular magnetic field. The total resistance of the wire and rail is 0.350ohms . Pulling the wire at a steady speed of 4.0m/s causes 4.20W of power to be dissipated in the circuit. part A: How big is the pulling force? part B: What is the strength of the magnetic field?

Answer 1

A) 1.05 N

The power dissipated in the circuit can be written as the product between the pulling force and the speed of the wire:

`P=Fv`

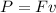
where

P = 4.20 W is the power

F is the magnitude of the pulling force

v = 4.0 m/s is the speed of the wire

Solving the equation for F, we find

`F=(P)/(v)=(4.20 W)/(4.0 m/s)=1.05 N`

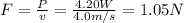
B) 3.03 T

The electromotive force induced in the circuit is:

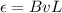`\epsilon=BvL` (1)

where

B is the strength of the magnetic field

v = 4.0 m/s is the speed of the wire

L = 10.0 cm = 0.10 m is the length of the wire

We also know that the power dissipated is

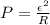`P=(\epsilon^2)/(R)` (2)

where

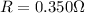`R=0.350 \Omega` is the resistance of the wire

Subsituting (1) into (2), we get

`P=(B^2 v^2 L^2)/(R)`

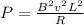
And solving it for B, we find the strength of the magnetic field:

`B=(√(PR))/(vL)=(√((4.20 W)(0.350 \Omega)))/((4.0 m/s)(0.10 m))=3.03 T`