Question

A function is in the form g(X) = ax^2 + d. If a is greater than 1 and d is negative, which could be the graph of g(x)?

Answer 1

Option B

Explanation:

Step-by-step explanation:

We have the function
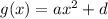`g(x)=ax^2 +d` then, by definition:

If
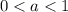`0 <a <1` then the graph is compressed vertically by a factor a.

If
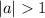`|a| > 1` then the graph is stretched vertically by a factor a

If
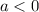`a <0` then the graph is reflected on the x axis.

If
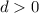`d> 0` the graph moves vertically upwards d units.

If
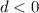`d <0` the graph moves vertically down d units.

We know that:

`a > 1` then the graph is stretched vertically by a factor a

and

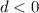`d <0` the graph moves vertically down d units

The searched graph is stretched vertically and its vertex is displaced downwards

The answer is option B