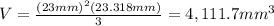Question

HELPPPP What is the volume of the square pyramid? Use Pythagorean’s Theorem to find the height of the pyramid

Answer 1

Answer: 4,111.7 mm³

Explanation:

You need to use this formula to calculate the volume of the square pyramid:

`V=(s^2h)/(3)`

Where "s" is the lenght of any side of the square base and "h" is the height of the pyramid.

Find the height with the Pythagorean Theorem:

`a^2=b^2+c^2`

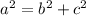
Where "a" is the hypotenuse and "b" and "c" are the legs of the right triangle. Let be "c" the height of the pyramid.

You can identify in the figure that:

`a=26mm\\\\b=(23mm)/(2)=11.5mm\\\\c=h`

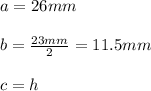
Then, you can find the height:

`(26mm)^2=(11.5mm)^2+h^2\\\\h=√((26mm)^2-(11.5mm)^2)\\\\h=23.318mm`

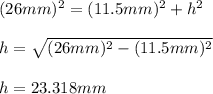
Then, knowing that:

`s=23mm\\h=23.318mm`

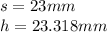
You can calculate the volume:

`V=((23mm)^2(23.318mm))/(3)=4,111.7mm^3`