Question

Point O is the center of the circle.
what is the area of the shaded portion of the circle

Answer 1

A 360 degree I think

Answer 2

The area of the shaded portion of the circle is option G. 28.5cm²

How did we get the value?

To find the shaded area of a circle, you need to know the radius of the circle and the central angle of the sector that forms the shaded region. The formula for the area of a sector (a portion of a circle) is given by:

`\[ \text{Area of Sector} = \left( \frac{\text{Central Angle}}{360^\circ} \right) * \pi r^2 \]`

where:

-
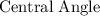`\( \text{Central Angle} \)` is the measure of the angle at the center of the circle (in degrees),

-
`\( \pi \)` is a mathematical constant approximately equal to 3.14159, and

-
`\( r \)` is the radius of the circle.

If the shaded region is not a complete sector but a segment (a portion of the circle bounded by a chord and an arc), you may need to subtract the area of the triangle formed by the radius and the two radii extending to the endpoints of the chord. The formula for the area of the segment is then:

`\[ \text{Area of Segment} = \text{Area of Sector} - \text{Area of Triangle} \]`

One can find the shaded area by:

1. Determine the radius
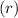`(\( r \))` of the circle.

2. Find the measure of the central angle
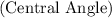`(\( \text{Central Angle} \))` of the sector or segment.

3. Apply the formula to calculate the area of the sector
`(\( \text{Area of Sector} \))`.

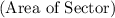4. If it's a segment, find the area of the triangle formed by the radii and the chord and subtract it from the area of the sector.

`\[ \text{Area of Quarter Circle} = (1)/(4) * \pi r^2 \]`

Given that the radius
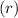`(\( r \))` is 10, you can substitute this value into the formula:

`\[ \text{Area of Quarter Circle} = (1)/(4) * \pi * (10)^2 \]`

Let's calculate this:

`\[ \text{Area of Quarter Circle} = (1)/(4) * \pi * 100 \]`

`\[ \text{Area of Quarter Circle} = (1)/(4) * 100 \pi \]`

`\[ \text{Area of Quarter Circle} = 25 \pi \]`

1/2 × 10 × 10 = 50cm²

25π - 50 = 25 × 3.14 - 50

= 78.5 - 50

= 28.5cm²