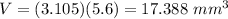Question

I need to find the surface area and volume of all three figures. If you could provide what equations you used to I will be grateful :)

Thank you <3

Answer 1

Part 1) Sphere The surface area is equal to
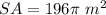`SA=196\pi\ m^(2)` and the volume is equal to
`V=(1,372)/(3)\pi\ m^(3)`

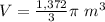
Part 2) Cone The surface area is equal to
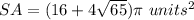`SA=(16+4√(65))\pi\ units^(2)` and the volume is equal to
`V=(112)/(3)\pi\ units^(3)`

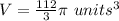
Part 3) Triangular Prism The surface area is equal to
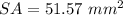`SA=51.57\ mm^(2)` and the volume is equal to
`V=17.388\ mm^(3)`

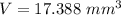
Explanation:

Part 1) The figure is a sphere

a) Find the surface area

The surface area of the sphere is equal to

`SA=4\pi r^(2)`

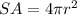
we have

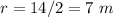`r=14/2=7\ m` ----> the radius is half the diameter

substitute

`SA=4\pi (7)^(2)`

`SA=196\pi\ m^(2)`

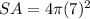
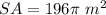
b) Find the volume

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

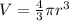
we have

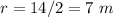`r=14/2=7\ m` ----> the radius is half the diameter

substitute

`V=(4)/(3)\pi (7)^(3)`

`V=(1,372)/(3)\pi\ m^(3)`

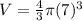
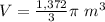
Part 2) The figure is a cone

a) Find the surface area

The surface area of a cone is equal to

`SA=\pi r^(2) +\pi rl`

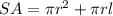
we have

`r=4\ units`

`h=7\ units`

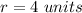
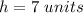
Applying Pythagoras Theorem find the value of l (slant height)

`l^(2)=r^(2) +h^(2)`

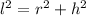
substitute the values

`l^(2)=4^(2) +7^(2)`

`l^(2)=65`

`l=√(65)\ units`

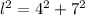
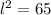
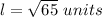
so

`SA=\pi (4)^(2) +\pi (4)(√(65))`

`SA=16\pi +4√(65)\pi`

`SA=(16+4√(65))\pi\ units^(2)`

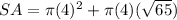
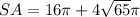
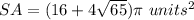
b) Find the volume

The volume of a cone is equal to

`V=(1)/(3)\pi r^(2)h`

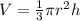
we have

`r=4\ units`

`h=7\ units`

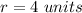
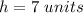
substitute

`V=(1)/(3)\pi (4)^(2)(7)`

`V=(112)/(3)\pi\ units^(3)`

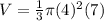
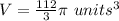
Part 3) The figure is a triangular prism

a) The surface area of the triangular prism is equal to

`SA=2B+PL`

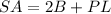
where

B is the area of the triangular base

P is the perimeter of the triangular base

L is the length of the prism

Find the area of the base B

`B=(1)/(2) (2.7)(2.3)=3.105\ mm^(2)`

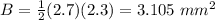
Find the perimeter of the base P

`P=2.7*3=8.1\ mm`

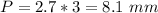
we have

`L=5.6\ mm`

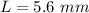
substitute the values

`SA=2(3.105)+(8.1)(5.6)=51.57\ mm^(2)`

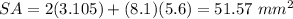
b) Find the volume

The volume of the triangular prism is equal to

`V=BL`

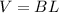
where

B is the area of the triangular base

L is the length of the prism

we have

`B=3.105\ mm^(2)`

`L=5.6\ mm`

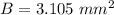
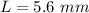
substitute

`V=(3.105)(5.6)=17.388\ mm^(3)`