Answer: First option
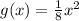
Explanation:
Step-by-step explanation:
If the graph of the function
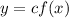 represents the transformations made to the graph of
represents the transformations made to the graph of
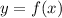 then, by definition:
then, by definition:
If
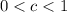 then the graph is compressed vertically by a factor c.
then the graph is compressed vertically by a factor c.
If
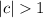 then the graph is stretched vertically by a factor c
then the graph is stretched vertically by a factor c
If
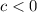 then the graph is reflected on the x axis.
then the graph is reflected on the x axis.
In this problem we have the function
 If this function is vertically compressed by a factor of 8 then
If this function is vertically compressed by a factor of 8 then
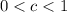 and
and

Therefore the graph of g(x) is
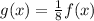
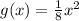
The answer is the first option