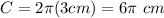Question

If the area of a circle measures 9π cm2, what is the circumference of the circle in terms of π?

A) 3π cm
B) 6π cm
C)
9/4
π cm
D)
9/2
π cm

Answer 1

B

Explanation:

The area (A) of a circle = πr² ← r is the radius

here A = 9π, hence

πr² = 9π ( divide both sides by π )

r² =
`(9\pi )/(\pi )` = 9

r =
`√(9)` = 3

The circumference (C) of a circle is C = 2πr, hence

C = 2π × 3 = 6π → B

Answer 2

Answer: option B

Explanation:

The circumference of a circle can be calculated with this formula:

`C=2\pi r`

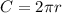
Where "C" is the circumference of the circle and "r" is the radius of the circle.

The area of a circle can be calculated with:

`A=\pi r^2`

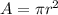
Where "r" is the radius.

Knowing the area, you can solve for the radius:

`r^2=(9\pi cm^2)/(\pi )\\\\r=\sqrt{(9\pi cm^2)/(\pi ) }\\\\r=3cm`

Substituting into
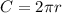`C=2\pi r`, you get that the circumference of this circle is:

`C=2\pi (3cm)=6\pi\ cm`