Question

Cylinder a has a radius of 1 m and a height of 4 m cylinder B has a radius of 1 m and a height of 8 m what is the ratio of the volume of cylinder a to the volume of cylinder B

a. 1:2
b. 2:1
c. 1:1
d. 1:4

Answer 1

Answer: option a

Explanation:

The volume of a cylinder can be calculated with this formula:

`V=\pi r^2h`

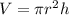
Where the radius is "r" and the height is "h"

Calculate the volume of the Cylinder A:

`V_A=\pi (1m)^2(4m)\\\\V_A=4\pi\ m^3`

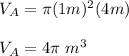
Calculate the volume of the Cylinder B:

`V_B=\pi (1m)^2(8m)\\\\V_B=8\pi\ m^3`

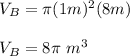
Now, the ratio of the volume of the Cylinder A to the volume of the Cylinder B can be calculated with:

`ratio=(V_A)/(V_B)`

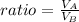
Substituting values, you get:

`ratio=(4\pi\ m^3)/(8\pi\ m^3)`

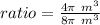
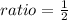`ratio=(1)/(2)` or 1:2