Answer: The correct option is
(A)
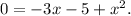
Step-by-step explanation: We are given to select the correct quadratic equation that has an a-value of 1, b-value of -3 and c-value of -5.
We know that
a general quadratic equation is of the following form :
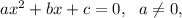
where a is the coefficient of x²,
b is the coefficient of x
and
c is the constant term.
For the given equation, we get
the coefficient of x², a = 1,
the coefficient of x, b = -3
and
the constant term, c = -5.
Therefore, the required equation is
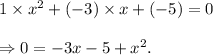
Thus, (A) is the correct option.