The 5th term in a geometric sequence is 40. The 7th term is 10. What is (are) the possible value(s) of the 4th term? Show all work

Question

asked Jan 20, 2020 34.7k views

1 Answer

Nikunj Dhimar · Answer 1 · 2020-01-24T17:23:40+0000

Answer:

possible values of 4th term is 80 & - 80

Explanation:

The general term of a geometric series is given by

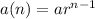
a(n)=ar^(n-1)

Where a(n) is the nth term, r is the common ratio (a term divided by the term before it) and n is the number of term

$ar^(5-1)=40\\ar^4=40$

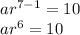
$ar^(7-1)=10\\ar^6=10$

We can solve for a in the first equation as:

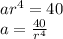
$ar^4=40\\a=(40)/(r^4)$

Now we can plug this into a of the 2nd equation:

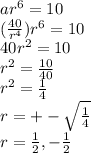
$ar^6=10\\((40)/(r^4))r^6=10\\40r^2=10\\r^2=(10)/(40)\\r^2=(1)/(4)\\r=+-\sqrt{(1)/(4)} \\r=(1)/(2),-(1)/(2)$

Let's solve for a:

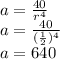
$a=(40)/(r^4)\\a=(40)/(((1)/(2))^4)\\a=640$

Now, using the general formula of a term, we know that 4th term is:

4th term = ar^3

Plugging in a = 640 and r = 1/2 and -1/2 respectively, we get 2 possible values of 4th term as:

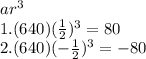
$ar^3\\1.(640)((1)/(2))^3=80\\2.(640)(-(1)/(2))^3=-80$

possible values of 4th term is 80 & - 80