Question

Which of the following is a solution of y - x < -3?

A. (6,2)

B. (2,6)

C. (2,-1)
Thanks

Answer 1

Option A. (6,2)

Explanation:

We have the following inequality:

`y- x <-3`

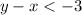
Solving for y we have:

`y<x-3`

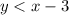
The line that limits the region of inequality is

`y = x-3`

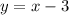
Then the region of inequality are all values of y that are less than
`f (x) = x-3`

In other words, the points belonging to the inequality are all those that lie below the line.

To find out which point belongs to this region substitute inequality and observe if it is satisfied

A. (6,2)

`2<6-3`

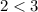`2<3` is satisfied

B. (2, 6)

`6<2-3`

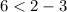
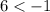`6<-1` it is not satisfied

C. (2, -1)

`-1<2-3`

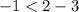
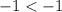`-1<-1` it is not satisfied

The answer is the option A