Answer:
(-6,4)
Explanation:
The equations are:
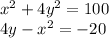
Solving for x^2 of the 2nd equation and putting that in place of x^2 in the 2nd equation we have:
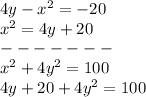
Now we can solve for y:
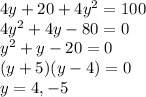
So plugging in y = 4 into an equation and solving for x, we have:
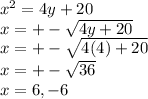
So y = 4 corresponds to x = 6 & x = -6
The pairs would be
(6,4) & (-6,4)
we see that (-6,4) falls in the 2nd quadrant, thus this is the solution we are looking for.