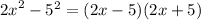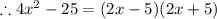Question

Help!! - 2.10 - (4 points)

1. Would you factor out the GCF, use the Perfect Square Trinomial pattern, or the Difference of Squares Pattern?
4x^2 - 25
2. Show how you would use the approach you picked by factoring this binomial.

Answer 1

Approach: Difference of Squares Pattern

`4 {x}^(2) - 25 = (2x - 5)(2x + 5)`

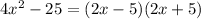
Explanation:

The given binomial is:

`4 {x}^(2) - 25`

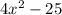
We can rewrite to obtain:

`{(2x)}^(2) - {5}^(2)`

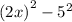
This is a difference of two squares, so we will factor using difference of squares pattern.

Recall that:

`{a}^(2) - {b}^(2) = (a + b)(a - )`

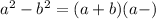
If we let

`a = 2x`

and

`b = 5`

Then we can factor the given binomial to obtain:

`{2x}^2 - {5}^(2) = (2x - 5)(2x + 5)`

`\therefore4 {x}^(2) - 25 = (2x - 5)(2x + 5)`