Question

The coach has 3 positions to fill on his basketball team. There are 9 students interested in being on the team. How many combinations of the three positions can he choose?

Answer 1

84

Explanation:

To find this, we need to understand the combination formula.

If we have n items and we want to choose r at a time, we use the formula:

`nCr=(n!)/((n-r)!*r!)`

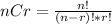
Where n! means n(n-1)(n-2)....

So we want 9C3, plugging them into the formula and doing some arithmetic, we have:

`nCr=(n!)/((n-r)!*r!)\\9C3=(9!)/((9-3)!*3!)\\=(9!)/(6!*3!)\\=(9*8*7*6!)/(6!*3*2*1)\\=(9*8*7)/(3*2*1)\\=84`

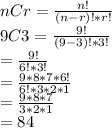
So, there can be 84 combinations possible.