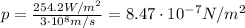Question

A plane electromagnetic wave, with wavelength 4.1 m, travels in vacuum in the positive direction of an x axis. The electric field, of amplitude 310 V/m, oscillates parallel to the y axis. What are the (a) frequency, (b) angular frequency, and (c) angular wave number of the wave? (d) What is the amplitude of the magnetic field component? (e) Parallel to which axis does the magnetic field oscillate? (f) What is the time-averaged rate of energy flow associated with this wave? The wave uniformly illuminates a surface of area 1.8 m2. If the surface totally absorbs the wave, what are (g) the rate at which momentum is transferred to the surface and (h) the radiation pressure?

Answer 1

(a)
`7.32\cdot 10^7 Hz`

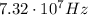
The frequency of an electromagnetic waves is given by:

`f=(c)/(\lambda)`

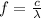
where

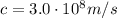`c=3.0\cdot 10^8 m/s` is the speed of light

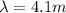`\lambda=4.1 m` is the wavelength of the wave in the problem

Substituting into the equation, we find

`f=(3.0\cdot 10^8 m/s)/(4.1 m)=7.32\cdot 10^7 Hz`

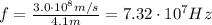
(b)
`4.60\cdot 10^8 rad/s`

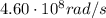
The angular frequency of a wave is given by

`\omega = 2\pi f`

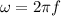
where

f is the frequency

For this wave,

`f=7.32\cdot 10^7 Hz`

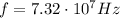
So the angular frequency is

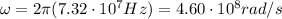
`\omega=2\pi(7.32\cdot 10^7 Hz)=4.60\cdot 10^8 rad/s`

(c)
`1.53 m^(-1)`

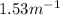
The angular wave number of a wave is given by

`k=(2\pi)/(\lambda)`

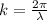
where

`\lambda` is the wavelength of the wave

For this wave, we have

`\lambda=4.1 m`

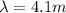
so the angular wave number is

`k=(2\pi)/(4.1 m)=1.53 m^(-1)`

(d)
`1.03\cdot 10^(-6)T`

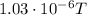
For an electromagnetic wave,

`E=cB`

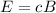
where

E is the magnitude of the electric field component

c is the speed of light

B is the magnitude of the magnetic field component

For this wave,

E = 310 V/m

So we can re-arrange the equation to find B:

`B=(E)/(c)=(310 V/m)/(3\cdot 10^8 m/s)=1.03\cdot 10^(-6)T`

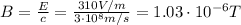
(e) z-axis

In an electromagnetic wave, the electric field and the magnetic field oscillate perpendicular to each other, and they both oscillate perpendicular to the direction of propagation of the wave. Therefore, we have:

- direction of propagation of the wave --> positive x axis

- direction of oscillation of electric field --> y axis

- direction of oscillation of magnetic field --> perpendicular to both, so it must be z-axis

(f) 127.5 W/m^2

The time-averaged rate of energy flow of an electromagnetic wave is given by:

`I=(E^2)/(2\mu_0 c)`

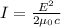
where we have

E = 310 V/m is the amplitude of the electric field

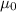`\mu_0` is the vacuum permeability

c is the speed of light

Substituting into the formula,

`I=((310 V/m)^2)/(2(4\pi\cdot 10^(-7) H/m) (3\cdot 10^8 m/s))=127.5 W/m^2`

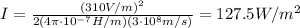
(g)
`1.53\cdot 10^(-8) kg m/s`

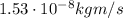
For a surface that totally absorbs the wave, the rate at which momentum is transferred to the surface given by

`(dp)/(dt)=(<S>A)/(c)`

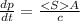
where the <S> is the magnitude of the Poynting vector, given by

`<S>=(EB)/(\mu_0)=((310 V/m)(1.03\cdot 10^(-6) T))/(4\pi \cdot 10^(-7)H/m)=254.2 W/m^2`

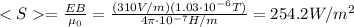
and where the surface is

A = 1.8 m^2

Substituting, we find

`(dp)/(dt)=((254.2 W/m^2)(1.8 m^2))/(3\cdot 10^8 m/s)=1.53\cdot 10^(-8) kg m/s`

(h)
`8.47\cdot 10^(-7) N/m^2`

For a surface that totally absorbs the wave, the radiation pressure is given by

`p=(<S>)/(c)`

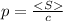
where we have

`<S>=254.2 W/m^2`

`c=3\cdot 10^8 m/s`

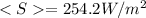
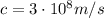
Substituting, we find

`p=(254.2 W/m^2)/(3\cdot 10^8 m/s)=8.47\cdot 10^(-7) N/m^2`