Answer: Y = 4x + 2
(It would be either the third or fourth choice since they are the same, one of them must be mistaken)
Explanation:
Given information
(x₁, y₁) = (1, 6)
(x₂, y₂) = (0, 2)
Find the slope through the formula
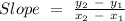
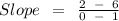
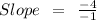

Substitute values into the linear form
Equation: y = mx + b
Point (0, 2)
y = mx + b
(2) = (4) (0) + b
2 = 0 + b
b = 2 - 0
b = 2
Therefore, the equation is
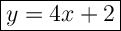
Hope this helps!! :)
Please let me know if you have any questions