Question

PLEASE HELP! If you apply the changes below to the quadratic parent function, f(x) = x2, what is the equation of the new function?

Shift 1 unit right.
Vertically stretch by a factor of 5
Reflect over the x-axis

Answer 1

Explanation:

By the way, please use the symbol " ^ " to indicate exponentiation:

f(x) = x^2

Shifted 1 unit to the right, we get g(x) = (x - 1)^2

Vertically stretched by a factor of 5, we get h(x) = 5(x - 1)^2

Reflected over the x-axis: j(x) = -5(x - 1)^2

Answer 2

The correct option is A.

Explanation:

The quadratic parent function is

`f(x)=x^2`

The translation is defined as

`g(x)=k(x+a)^2+b` .... (1)

Where, k is vertical stretch, a is horizontal shift and b is vertical shift.

If |k|>1, then graph of parent function stretch vertically by factor |k| and if 0<|k|<1, then parent function compressed vertically by factor |k|. Negative k represents the reflection across x axis.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

The graph shift 1 unit right,vertically stretch by a factor of 5 , reflect over the x-axis. So, a=-1, |k|=5 and k=-5

Substitute a=-1 and k=5 in equation (1).

`g(x)=-5(x+(-1))^2+(0)`

`g(x)=-5(x-1)^2`

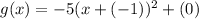
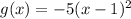
Therefore the correct option is A.