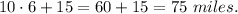Answer:
75 miles
Explanation:
Let x mph be the cyclist A rate, then x+3 mph is the cyclist B rate.
1. In 1 hour they both traveled x+x+3=2x+3 miles. In 5 hours they traveled
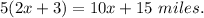
2. Cyclist A spent
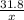 hours to travel 31.8 miles. If the cyclist from B had started moving 30 minutes (1/2 hour) later than the cyclist A, then he spent
hours to travel 31.8 miles. If the cyclist from B had started moving 30 minutes (1/2 hour) later than the cyclist A, then he spent
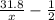 hours to travel the rest of the distance. In total they both traveled the whole distance 10x+15 miles, thus
hours to travel the rest of the distance. In total they both traveled the whole distance 10x+15 miles, thus
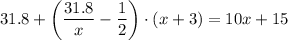
Solve this equation. Multiply it by 2x:
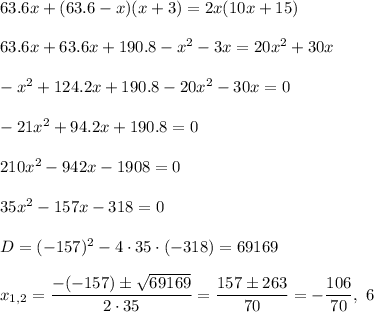
The rate cannot be negative, thus, x=6 mph.
Hence, the distance between cities A and B is