Question

Write this expression into a single log:
Ln10 - Ln2 + Ln3​

Answer 1

ln15 or ≈ 2.708

Explanation:

we can use the rules of logarithms to condense the logarithm

ln10 - ln2 + ln3

looking at the expression from left to right we see the first 2 terms: ln10 - ln2

we can use the quotient rule where log base b (x/y) = log base b x - log base b y. in other words, the quotient rule allows us to write a subtraction of 2 logarithims with the same base as a division

ln10 and ln2 have the same base e, so we can write them as a division

`(ln10)/(ln2)`

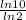
so we have the expression:
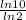`(ln10)/(ln2)` + ln3

we can simplify
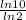`(ln10)/(ln2)` to equal ln5, as 10/2 = 5

the new expression is ln5 + ln3

next, we can use the product rule where log base b (x)(y) = log base b x + log base b y. in other words, 2 logarithims with the same base added together can be written as a multiplication

ln5 and ln3 have the same base, so we will write them as a multiplication

(ln5)(ln3) = ln15

our final answer is ln15, which can be simplified if needed in decimal form as ≈ 2.708