Answer:
7,400
Explanation:
First, we have to see that this is an arithmetic sequence... since to get the next element we add 1 to it. (a geometric sequence would be a multiplication, not an addition)
So, we have a, the first term (a = 53), and we have the difference between each term (d = 1), and we want to find the SUM of the first 80 terms.
To do this without spending hours writing them down, we can use this formula:
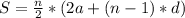
If we plug in our values, we have:
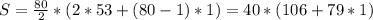
S = 40 * (106 + 79) = 40 * 185= 7,400