Answer:
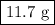
Step-by-step explanation:
We are given the amounts of two reactant solutions, so this is a limiting reactant problem.
We know that we will need a balanced equation with masses, moles, and molar masses, so, let's assemble our information in one place, with molar masses above the formulas and the
M_r: 234.77
2AgNO₃ + CaI₂ ⟶ 2AgI + Ca(NO₃)₂
Solution: (50.00 mL, 1.00 M) (30.00 mL, 1.25 M)
Step 1. Calculate the moles of each reactant
Moles of AgNO₃ = 50.00 mL × (1.00 mmol/1 mL) = 50.00 mmol
Moles of CaI₂ = 30.00 mL × (1.25 mmol/1 mL) = 37.50 mmol
Step 2. Identify the limiting reactant
Calculate the moles of AgI we can obtain from each reactant.
From AgNO₃:
The molar ratio of AgI:AgNO₃ is 2:2.
Moles of AgI = 50.00 mmol AgNO₃ × (2 mmol AgI/2 mmol AgNO₃)
= 50.00 mmol AgI
From CaI₂:
The molar ratio of AgI:CaI₂ is 2:1.
Moles of CaI₂ = 37.50 mmol × (2 mmol AgI/1 mmol CaI₂) = 75.00 mmol AgI
AgNO₃ is the limiting reactant because it gives the smaller amount of AgI.
Step 3. Calculate the mass of AgI.
Mass = 50.00 mmol AgI × (234.77 mg AgI /1 mmol AgI)
= 11 700 mg AgI = 11.7 g AgI
The mass of silver iodide formed is
 .
.