Question

A traffic camera sits on top of a tower that has a height of 50ft., the angles of depression of two cars on a straight road at the same level as that of the base of the tower and on the same side of it are 25° and 40°. Calculate the distance between two cars

Answer 1

`\boxed{\text{48 ft}}`

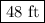
Explanation:

The angle of depression from the camera at D and the angle of elevation from the target cars are congruent.

1. Distance of car A from tower

Consider ∆ACD

tan25 = 50/AC

AC = 50/tan25 = 50/0.4663 = 107.2 ft

2. Distance of car B from tower

Consider ∆BCD

tan40 = 50/BC

AC = 50/tan40 = 50/0.8391 = 59.6 ft

3. Distance from cars A and B

AB = AC – BC = 107.2 – 59.6 = 48 ft

The distance between the two cars is
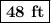`\boxed{\textbf{48 ft}}`.