Answer: Option C

Explanation:
Whenever we have a main function f(x) and we want to transform the graph of f(x) by moving it vertically then we apply the transformation:

If
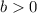 then the graph of k(x) will be the graph of f(x) displaced vertically b units down.
then the graph of k(x) will be the graph of f(x) displaced vertically b units down.
If
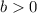 then the graph of k(x) will be the graph of f(x) displaced vertically b units upwards.
then the graph of k(x) will be the graph of f(x) displaced vertically b units upwards.
In this case we have
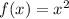
We know that this function has its vertex in point (0,0).
Then, to move its vertex 7 units down we apply the transformation:
 .
.
Then the function k(x) that will have its vertex 7 units below f(x) is
