Answer:
Option D (7, -3)
Explanation:
We know that the general equation of an ellipse has the form:
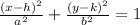
Where the point (h, k) are the coordinates of the center of the ellipse
In this case the equation of the ellipse is:

Then
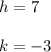
So The coordinates of the center of the ellipse are (7, -3)