Answer:
Second Option
671 m²; 725 m²
Explanation:
The lateral area of a triangular prism is:
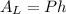
Where P is the perimeter of the triangular base and h is the height of the prism.
In this case, the perimeter of the triangular base is:

Then the height is 26 m
Then the lateral area of the prism is:
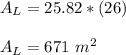
Therefore the surface area of the triangular prism is:
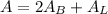
Where
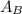 is the area of the base.
is the area of the base.
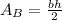
Where b is the base of the triangle and h is the height
In this case:

Finally

The answer is 671 m² and 725 m²