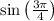Answer:

Explanation:
Angle
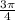 lies in second quadrant in which
lies in second quadrant in which
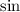 is positive .
is positive .
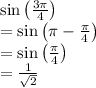
We know that
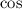 is positive in first and fourth quadrant .
is positive in first and fourth quadrant .
In first quadrant :
We know that angle
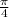 lies in first quadrant .
lies in first quadrant .

In fourth quadrant :
We know that angle
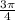 lies in fourth quadrant.
lies in fourth quadrant.

So, for angles
 ,
,
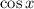 has the same value as
has the same value as