Answer:
Part 1) option a.
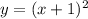
Part 2) option c.

Part 3) option a. Yes , d=-2
Part 4) option b.
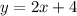
Part 5) option b.
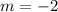
Part 6) option c.

Part 7) option c.
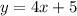
Part 8) option a. y=2x-1 and y=x+1
Explanation:
Part 1)
we know that
If a ordered pair satisfy a function, then the function pass through the ordered pair
Verify each function with the points (1,4), (2,9) and (3,16)
case a) we have
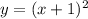
For x=1, y=4
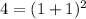
 ----> is true
----> is true
For x=2, y=9
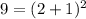
 ----> is true
----> is true
For x=3, y=16
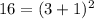
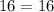 ----> is true
----> is true
therefore
The function pass through the three points
case b) we have
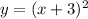
For x=1, y=4
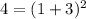
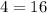 ----> is not true
----> is not true
therefore
The function not pass through the three points
case c) we have
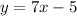
For x=1, y=4
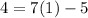
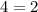 ----> is not true
----> is not true
therefore
The function not pass through the three points
Part 2)
Let
y------> the number of laps
x-----> the number of hours
we know that
The linear equation that represent this situation is

Part 3) we have
{4,2,0,-2,-4,-6,...}
Let
a1=-4
a2=2
a3=0
a4=-2
a5=-4
a6=-6
we know that
a2-a1=2-4=-2 -----> a2=a1-2
a3-a2=0-2=-2 ----> a3=a2-2
a4-a3=-2-0=-2 -----> a4=a3-2
a5-a4=-4-(-2)=-2----> a5=a4-2
a6-a5=-6-(-4)=-2----> a6=a5-2
therefore
Is an arithmetic sequence, the common difference is -2
Part 4) we know that
The y-intercept of the graph is (0,4)
The x-intercept of the graph is (-2,0)
therefore
the function is
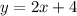
because
For x=0 -----> y=2(0)+4 -----> y=4
For y=0 ----> 0=2x+4 --------> x=-2
Part 5) we know that
The formula to calculate the slope between two points is equal to
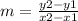
we have
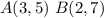
substitute the values
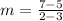
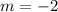
Part 6) we know that
The equation of the line into slope point form is equal to

we have

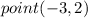
substitute the values
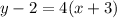
Convert to slope intercept form
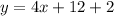

Part 7) we know that
If two lines are parallel, then their slopes are the same
The equation of the given line is
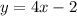
so
The slope of the given line is

therefore
The line
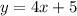 is parallel to the given line
is parallel to the given line
Because the slope is equal to

Part 8) we know that
If a ordered pair is a solution of a system of equations, then the ordered pair must satisfy both equations of the system
Verify each case for (2,3)
case a)
y=2x-1 -----> equation 1
y=x+1 -----> equation 2
Substitute the value of x and the value of y in each equation and then compare the results
Verify equation 1
3=2(2)-1
3=3 -----> is true
Verify equation 2
3=2+1
3=3 -----> is true
therefore
The point (2,3) is a solution of the system of equations case a
case b)
y=2x+1 -----> equation 1
y=x-1 -----> equation 2
Substitute the value of x and the value of y in each equation and then compare the results
Verify equation 1
3=2(2)+1
3=5 -----> is not true
therefore
The point (2,3) is not a solution of the system of equations case b
case c)
y=4x-5 -----> equation 1
y=2x -----> equation 2
Substitute the value of x and the value of y in each equation and then compare the results
Verify equation 1
3=4(2)-5
3=3 -----> is true
Verify equation 2
3=2(2)
3=4 -----> is not true
therefore
The point (2,3) is not a solution of the system of equations case c