Question

Trapezoid FGHJ is inscribed in P as shown. If FG = 24, JH = 10, and the diameter of P is 26, find the area of the trapezoid. (Hint: draw in auxiliary lines). Round to the nearest tenth if necessary.

Answer 1

221

Explanation:

If the diameter is 26, the radius is 13 (which is the same as the perpendicular from P to JH)

So, the area is

`(1)/(2)(13)(24+10)=221`

Answer 2

The area of a trapezoid is 289 square units

The center of the circle as P, and let the points where the trapezoid intersects the circle be F,G,H, and J (in order).

Let the midpoint of the trapezoid's shorter base, JH is M, and longer base FG is N.

Step 1 :-

From right angle triangle ΔPMJ

The radius of the circle (JP): Given that the diameter is 26, the radius is half of that, which is 13.

JP = 13(radius), JM =5(M is the midpoint of JH), PM = ?

Use the Pythagorean Theorem in triangle ΔPMJ

`JP^2 = JM^2 + PM^2`

`13^2 = 5^2 + PM^2`

`PM = 12`

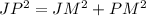
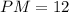
Step 2 :-

From right angle triangle ΔPNF

The radius of the circle (PF): Given that the diameter is 26, the radius is half of that, which is 13.

PF = 13(radius), FN =12 (N is the midpoint of FG), NP = ?

Use the Pythagorean Theorem in triangle ΔPNF

`PF^2 = FN^2 + NP^2`

`13^2 = 12^2 + NP^2`

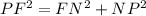
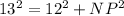
NP = 5

The height of the trapezoid (h): The height of the trapezoid is the perpendicular distance between FG and JH

h = NP + PM

h = 17

The area of a trapezoid: Area =
`(1)/(2) (b1 + b2) * h`

Area =
`(1)/(2) (24 + 10)*17`

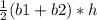
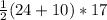
Area = 289 square units

Therefor The area of a trapezoid is 289 square units.