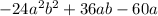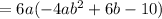Answer:
Explanation:
To solve these equations involving variables and exponents we need to follow these steps.
1) We need to find out the factor that is common in the equation.
2) After taking common, solve the equation. We can add or subtract only those values that have same bases.
1)
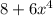
here we can see, both numbers are divisible by 2, so taking 2 common
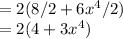
It cannot be further simplified because both number donot have same bases.
3.
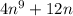
We can take 4n common
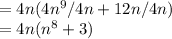
5. -12a -3
Here -3 cam be taken common
= -3(-12a/-3 -3/-3)
= -3(4a +1)
7.
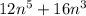
here the smallest power of n is n^3 so, we can take n^3 common and both coefficients are divisible by 4 so taking 4n^3 common

9.
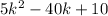
Here we cannot take k common, as k is not a multiple of 10. For taking common it should be divisible by each value in the equation. But each value s divisible by 5 so, taking 5 common
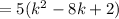
11.
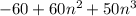
Here we cannot take n common, as n is not a multiple of -60. For taking common it should be divisible by each value in the equation. But each value s divisible by 10 so, taking 10 common

13.
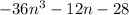
Here we cannot take n common, as n is not a multiple of 28. For taking common it should be divisible by each value in the equation. But each value s divisible by -4 so, taking -4 common
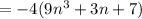
15.
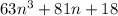
Here we cannot take n common, as n is not a multiple of 18. For taking common it should be divisible by each value in the equation. But each value s divisible by 9 so, taking 9 common
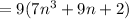
17.