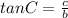Answer:
1 → D
2 → A
3 → B
4 → C
Explanation:
You need to remember that:

Then:
-For angle B, you can identify in the figure that:
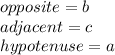
Then, you can substitute values and get:
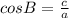
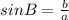
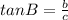
- For angle C, you can identify in the figure that:
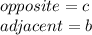
Therefore, substituting values, you get that: