Hello!
The answer is:
The equation of the new line will be:
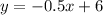
or
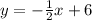
Why?
To solve the problem, we need to remember the slope intercept form of a line.
The slope intercept form of a line is given by the following equation:

Where,
y, is the function.
x, is the variable of the function.
m, is the pendant of the line.
b, is the y-axis intercept of the line.
So, we are given the line that will be parallel to the line that we are looking for:
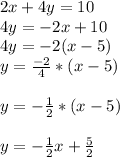
Where,
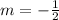
Then,
We need to use the same slope to guarantee that the new line will be parallalel to the given line-
So, our new line will have the following form:
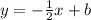
We need to substitute the given point to isolate "b" in order to guarantee that the line will pass through.
Now, substituting the given point, to calculate"b", we have:
Calculating b, we have:
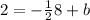
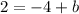
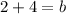
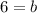
Hence, we have that the equation of the new line will be:
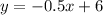
or
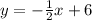
Proving that the line will pass through the given point, by substituting it into its equation, we have:
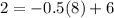
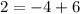
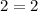
So, since the equality is satisfied, we know that the line pass through the new line.
Have a nice day!