Question

Please help!! 20 POINTS

Answer 1

Hello!

The answers are:

First image:

The answer is the second option, the angles is
`53\°`

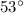
Second image:

The answer is the third option:

`(5)/(13)`

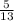
Third image:

The length of the adjacent leg is the first option:

`8√(2)units`

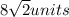
Fourth image:

The answer is the fourth option,
`72\°`

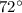
Fifth image:

The answer is the fourth option, DF (hypothenuse) is equal to 25 units.

Why?

To solve these problems, we need to use the following trigonometric identities and the Pythagorean Theorem, since we are working with right triangles.

`Tan(\alpha)=(y)/(x)\\\\(Tan(\alpha))^(-1) =((y)/(x))^(-1)\\\\\alpha =Arctan((y)/(x))`

`Sin(\alpha)=(opposite)/(hypothenuse)`

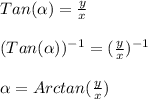
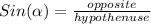
Pythagorean Theorem:

`c^(2)=a^(2) +b^(2)`

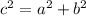
So, solving we have:

First image:

We are given a right triangle that has the following lengths:

`base=x=6units\\height=y=8units\\hypothenuse=10units`

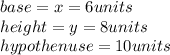
Then, calculating we have:

`\alpha =Arctan((y)/(x))\\\\\alpha =Arctan((8)/(6))\\\\\alpha =Arctan(1.33)\\\\\alpha =53\°`

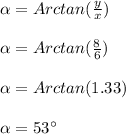
Hence, the answer is the second option, the angles is
`53\°`

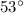
Second image:

We are given a right triangle that has the following lengths:

`base=x=12units\\height=y=5units\\hypothenuse=13units`

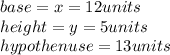
Then calculating the sin ratio, we have:

`Sin(\alpha)=(opposite)/(hypothenuse)`

`Sin(\alpha)=(5)/(13)`

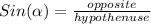
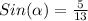
Thence, the answer is the third option:

`(5)/(13)`

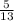
Third Image:

We are given the following information:

`hypothenuse=16units\\\\\alpha =45\°`

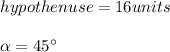
Then, calculating one of the angle legs, since both will have the same length, using the sine trigonometric identity, we have:

`Sin(\alpha)=(Opposite)/(Hypothenuse)\\ \\Sin(45\°)=(Opposite)/(16)\\\\Opposite=Sin(45\°)*16\\\\Opposite=(√(2) )/(2)*16=8√(2)`

Hence, the answer is the first option the length of the adjacent leg is

`Opposite=(√(2) )/(2)*16=8√(2)units`

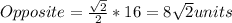
Fourth image:

We are given the following information:

`base=x=9units\\height=y=3units`

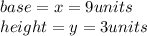
To calculate the angle at the B vertex, first, we need to calculate the angle at the C vertex, and then, calculate the B vertex by the following way:

Since the sum of all the interior angles of a triangle are equal to 180°, we have that:

`180\°=Angle_(B)+Angle{C}+90\°`

`Angle_(B)=180\° -90\°-Angle_(C)`

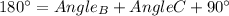
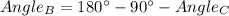
So, calculating the angle at the C vertex, we have:

`\alpha =Arctan((y)/(x))`

`\alpha =Arctan((3)/(9))`

`\alpha =Arctan(0.33)=18.26\°`

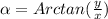
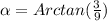
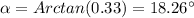
Then, calculating the angle at the B vertex, we have:

`Angle_(B)=180\° -90\°-18.26\°=71.74\°=71.8\°=72\°`

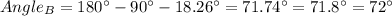
Hence, the answer is the fourth option,
`72\°`

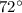
Fifth image:

We are given the following information:

`base=x=24units\\height=y=7units`

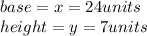
Now, to calculate the distance DF (hypothenuse) we need to use the Pythagorean Theorem:

`c^(2)=a^(2) +b^(2) \\\\hypothenuse^(2)=adjacent^(2)+opposite^(2)\\\\\sqrt{hypothenuse^(2)}=\sqrt{adjacent^(2)+opposite^(2)}\\\\hypothenuse=\sqrt{adjacent^(2)+opposite^(2)}`

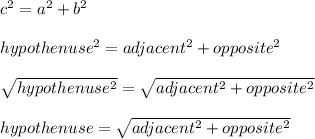
Then, substituting we have:

`hypothenuse=\sqrt{24^(2)+(7)^(2)}`

`hypothenuse=√(576+49)=√(625)`

`hypothenuse=√(625)`

`hypothenuse=25units`

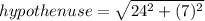
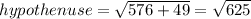
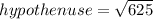
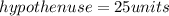
Hence, the answer is the fourth option, DF (hypothenuse) is equal to 25 units.

Have a nice day!