Question

Which of the following equations will produce the graph below?

Answer 1

The equation that represents the given graph is:

`6x^2+6y^2=144`

Explanation:

By looking at the given graph we observe that the graph is a circle with center at (0,0) and the radius is close to 5.

Now, we know that:

The general equation of a circle with center (h,k) and radius r is given by:

`(x-h)^2+(y-k)^2=r^2`

Here (h,k)=(0,0)

Hence, the equation of the circle is:

`x^2+y^2=r^2`

A)

`(x^2)/(20)+(y^2)/(20)=1\\\\i.e.\\\\x^2+y^2=20`

i.e.

`x^2+y^2=(2√(5))^2`

This equation is a equation of a circle with center at (0,0)

and radius is:
`2√(5)\ units`

i.e. the radius is approximately equal to 4.5 units.

But the radius is close to 5.

Hence, option: A is incorrect.

B)

`20x^2-20y^2=400\\\\i.e.\\\\x^2-y^2=20`

This is not a equation of a circle.

This equation represents a hyperbola.

Hence, option: B is incorrect.

C)

`x^2+y^2=16`

which could be represented by:

`x^2+y^2=4^2`

i.e. the radius of circle is: 4 units

which is not close to 5.

Hence,option: C is incorrect.

D)

`6x^2+6y^2=144`

On dividing both side of the equation by 6 we get:

`x^2+y^2=24`

i.e.

`x^2+y^2=(√(24))^2`

i.e.

Radius is:
`√(24)\ units`

which is approximately equal to 4.9 units which is close to 5 units.

Answer 2

Hello!

The answer is:

The equation D will produce the shown circle.

`6x^(2)+6y^(2)=144`

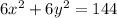
Why?

Since the graph is showing a circle, we need to find the equation of a circle that has a radius which is between 0 and 5 units, and has a center located at the origen (0,0).

Also, we need to remember the standard form of a circle:

`(x+h)^(2) +(y+k)^(2)=r^(2)`

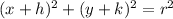
Where,

x, is the x-coordinate of the x-intercept point

y, is the y-coordinate of the y-intercept point

h, is the x-coordinate of the center.

k, is the y-coordinate of the center.

r, is the radius of the circle.

So, discarding each of the given options, we have:

First option:

A.

`(x^(2) )/(20)+ (y^(2) )/(20)=1\\\\(1)/(20)(x^(2)+y^(2))=1\\\\x^(2)+y^(2)=20*1\\\\x^(2)+y^(2)=20`

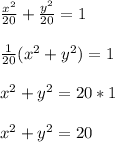
Where,

`radius=√(20)=4.47=4.5`

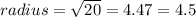
Now, can see that even the center is located at the point (0,0), the radius of the circle is equal to 4.5 units and from the graph we can see that the radius of the circle is more than 4.5 units but less than 5 units, the option A is not the equation that produces the shown circle.

Second option:

B.

`20x^(2) -20y^(2)=400\\\\(1)/(20)(x^(2) -y{2})=400\\\\x^(2) -y{2}=400*20`

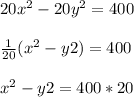
Where,

`radius=√(8000)=89.44units`

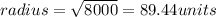
We can see that even the center is located at the point (0,0), the radius of the circle is 89.44 units, so, the option B is not the equation that produces the shown circle.

Third option:

C.

`x^(2)+y^(2)=16`

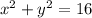
Where,

`radius=√(16)=4units`

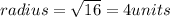
We can see that even the center is located at the point (0,0), the radius of the circle is 4 units, which is less than the radius of the circle shown in the graph, so, the option C is not the equation that produces the shown circle.

D.

`6x^(2)+6y^(2)=144\\\\6(x^(2) +y^(2))=144\\\\x^(2) +y^(2)=(144)/(6)=24\\\\`

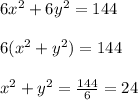
Where,

`radius=√(24)=4.89units`

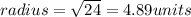
Now, we have that the radius of the circle is 4.89 units, which is approximated equal to 0, also, the center of the circle is located at (0,0) so, the equation D will produce the shown circle.

`6x^(2)+6y^(2)=144`

Have a nice day!