Question

Please help and look at the picture

Answer 1

Hello!

The answer is:

D.
`8\sqrt[3]{5}`

Why?

To solve the problem, we need to remember the following roots properties:

`a^{(m)/(n) }=\sqrt[n]{a^(m) }`

`a\sqrt[n]{b} =\sqrt[n]{a^(n)*b} \\\\\sqrt[n]{ab}=\sqrt[n]{a}*\sqrt[n]{b}`

So, we are given the expression:

`(8.320)^{(1)/(3) }`

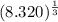
Then, writing its equivalent expression, we have:

`\sqrt[3]{8.320}`

Now, simplyfing, we have:

`\sqrt[3]{8.320}=\sqrt[3]{2560}=\sqrt[3]{512*5}\\\\\sqrt[3]{8.320}=\sqrt[3]{512*5}=\sqrt[3]{8^(3) .5}\\\\\sqrt[3]{8.320}=\sqrt[3]{8^(3) .5}=\sqrt[3]{8}*\sqrt[3]{5} \\\\\sqrt[3]{8.320}=\sqrt[3]{8}*\sqrt[3]{5}=8*\sqrt[3]{5}`

Hence, we have that the correct option is:

D.
`8\sqrt[3]{5}`

Have a nice day!