Answer:
![\sqrt[6]{2}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4cgs7owr0q5h31nk9x27znst671vf2mx5p.png)
Explanation:
write the equivalent expression for
![\frac{√(2)}{\sqrt[3]{2}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/odkn6jbi16dtl2mevojdoad14gahraqrqe.png)
to simplify it we need to rationalize the denominator
we multiply top and bottom by
![\sqrt[3]{4}](https://img.qammunity.org/2020/formulas/mathematics/college/74bherk11k3nniztwzxndphe3fyj3ycnwr.png)
![\frac{√(2)*\sqrt[3]{4}}{\sqrt[3]{2}*\sqrt[3]{4}}](https://img.qammunity.org/2020/formulas/mathematics/college/5gce9f3aax9qd9pxauvsobsi8iva2tdlu9.png)
![\frac{√(2)*\sqrt[3]{4}}{\sqrt[3]{8}}](https://img.qammunity.org/2020/formulas/mathematics/college/31rl2ftza7mxda8qt6u5h4rhgl2nlgsebs.png)
![\frac{√(2)*\sqrt[3]{4}}{2}](https://img.qammunity.org/2020/formulas/mathematics/college/adpvhjp0clbdqdauql6atewy7c3o84w7ow.png)
square root can be written as 1/2 and then cube root can be written as 1/3
![\sqrt[3]{4} =2^(2)/(3)](https://img.qammunity.org/2020/formulas/mathematics/college/wkd8707il4ufkbsnwey62agvs89w32fgik.png)
![\frac{√(2)*\sqrt[3]{4}}{2}](https://img.qammunity.org/2020/formulas/mathematics/college/adpvhjp0clbdqdauql6atewy7c3o84w7ow.png)
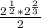
Now add the fractions
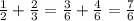
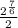
![\frac{\sqrt[6]{2^7}}{2}](https://img.qammunity.org/2020/formulas/mathematics/college/zhl8nydaq3nage3iolmz8r3k4absdc054h.png)
![\frac{2\sqrt[6]{2}}{2}](https://img.qammunity.org/2020/formulas/mathematics/college/367oy02sofrokc65293v7ezid8aa0jbmzw.png)
cancel out 2 at the top and bottom
![\sqrt[6]{2}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4cgs7owr0q5h31nk9x27znst671vf2mx5p.png)