Question

The data given for a football kicked from the field follows a quadratic model, h(x) = - 3x2 + 18x +7 . Where h(t) is the height in feet and t is the in seconds. Using this model, at what time will the ball reach its maximum height

Answer 1

three seconds

Explanation:

Answer 2

The time at which the ball will reach its maximum height is t= 3 seconds.

Explanation:

To find the the time at which the ball will reach its maximum height, we need to solve the model given - 3x2 + 18x +7

since h(t) is the height given we can re-write the equation as:

h(t)= -3(t)² + 18t +7

Differentiating the above equation

`(dt)/(dh) = -6t + 18`

When the ball is at maximum height
`(dt)/(dh)=0`

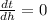
0=-6t+18

-18 = -6t

=> t= -18/-6

=> t= 3

the time at which the ball will reach its maximum height is t= 3 seconds.

We can find the maximum height by putting value of t in equation:

h(3) = -3(3)²+ 18(3) +7

h(3)= -27 + 54 + 7

h(3)= 34 ft