Question

Devontre rode his bike uphill 5 miles and then back downhill. The rate at which Devontre traveled downhill was 20 mph faster than his rate going uphill. If it took him 20 minutes longer to ride uphill than downhill, what was his uphill rate?

Answer 1

10 mph

Explanation:

Let x mph be Devontre rate uphill, then x+20 mph its his rate downhill.

1. Time uphill:

`(5)/(x)\ hours`

2. Time downhill:

`(5)/(x+20)\ hours`

3. If it took him 20 minutes (1/3 hour) longer to ride uphill than downhill, then

`(5)/(x)-(5)/(x+20)=(1)/(3)`

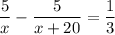
Solve this equation:

`(5(x+20)-5x)/(x(x+20))=(1)/(3)\\ \\(100)/(x(x+20))=(1)/(3)\\ \\300=x(x+20)\\ \\x^2+20x-300=0\\ \\D=20^2-4\cdot (-300)=400+1200=1600\\ \\x_(1,2)=(-20\pm √(1600))/(2)=(-20\pm 40)/(2)=-30,\ 10.`

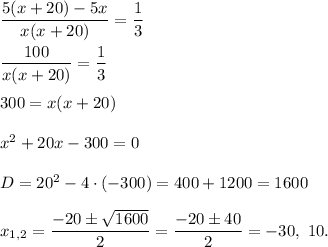
The rate cannot be negative, thus, x=10 mph (rate uphill).