Answer:
Option A.
Explanation:
Algebraically expressed function is f(x) = -8x² + 4x + 2
As we know in a quadratic equation f(x) = ax² + bx + c, if a is negative then the vertex will be maximum.
and the maximum value will be represented by
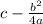
From the given quadratic equation
a = -8
b = 4 and c = 2
Now we place these values in the equation.
Maximum =
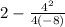
= 2 + 0.5
= 2.5
From the graph attached we can easily conclude that vertex of the parabola is less than 0.5
Therefore, algebraic function has the greater maximum value.
Option A. is the answer.