Question

Please check out my question
Thank u soo much

Answer 1

Answer: 1. C) (4, 5)

2. D) (3, 4)

3. B) 5/2

Explanation:

Plug in the (x, y) coordinates to see which makes a true statement for both of the given inequalities.

y ≥ -2x + 11 and y > 3x - 9

A) (2, 1) 1 ≥ -2(2) + 11 → 1 ≥ 7 is false

B) (4, 1) 1 ≥ -2(4) + 11 → 1 ≥ 3 is false

C) (4, 5) 5 ≥ -2(4) + 11 → 5 ≥ 3 is TRUE 5 > 3(4) - 9 → 5 > 3 is TRUE

D) (6, 6) 6 ≥ -2(6) + 11 → 6 ≥ -1 is TRUE 6 > 3(6) - 9 → 6 > 9 is false

The only option that produces a TRUE statement for both inequalities is C

********************************************************************************************

`y=(k)/(x)\qquad \implies \qquad x\cdot y=k`

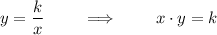
Given (2, 6), the k-value is 2 · 6 = 12.

Which (x, y) coordinates have a product of 12?

A) (1, 3) --> 1 · 3 = 3

B) (1, 4) --> 1 · 4 = 4

C) (3, 3) --> 3 · 3 = 9

D) (3, 4) --> 3 · 4 = 12 THIS WORKS!

********************************************************************************************

In order for the equation to have infinite solutions, the left side must equal the right side. Solve for "c"

8x - 2x(c + 1) = x

-2x(c + 1) = -7x subtracted 8x from both sides

c + 1 = (-7x)/(-2x) divided both sides by -2x

c + 1 = 7/2 simplified

c = 5/2 subtracted 1 from both sides