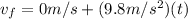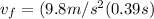Question

A cup falls off of a table from a height of 0.75m. What is the impact speed of the cup?

Answer 1

3.822 m/s

Step-by-step explanation:

You can solve this by using the kinematic equations:

`v_(f) = v_(i)+gt`

`d = v_it*(1)/(2)gt^(2)`

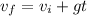
Where:

Vf = final velocity (impact velocity)

Vi = initial velocity

g = acceleration due to gravity

d = distance traveled

t = time

Acceleration due to gravity on Earth is constant. Gravity accelerates objects towards the ground at 9.8m/s².

Initial velocity is always at 0 m/s in free fall. Let's see what we have as our given:

d = 0.75m

Vi = 0 m/s

g = 9.8 m/s²

Look at our equation for the impact velocity (Vf) with our current given plugged in:

`v_(f)=v_(i)+gt`

`v_(f)=0m/s+(9.8m/s^(2))(t)`

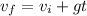
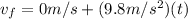
We still do not have time. That is where the second equation comes in. We plug in our values again in the secon equation and derive time:

`d=v_(i)t+(1)/(2)gt^(2)\\\\0.75m=0m/s(t)+(1)/(2)(9.8m/s^(2))(t^(2))\\\\0.75m = 0+(4.9m/s^(2))(t^(2))\\\\(0.75m)/(4.9m/s^(2))=t^(2)\\\\\sqrt{ 0.15s^(2)}=\sqrt{t^(2)}\\\\0.39s=t`

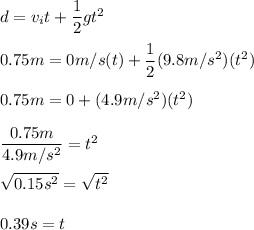
So our time is 0.39s. Now we use this in our first equation:

`v_(f)=0m/s+(9.8m/s^(2))(t)`

`v_(f)=(9.8m/s^(2)(0.39s)`

`v_(f)=3.822m/s`