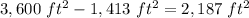Question

PLEASE HELP! Daniela has a rectangular yard with a pool in the shape of a semicircle. How many square feet of grass does Daniela need to cover her yard, but not the pool?

Answer 1

Part 1) Area of rectangle
`3,600\ ft^(2)`

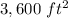
Part 2) Area of semicircle
`1,413\ ft^(2)`

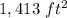
Par 3) Total area of grass
`2,187\ ft^(2)`

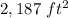
Explanation:

we know that

The total area of grass is equal to the area of rectangle minus the area of semicircle

step 1

Find the area of rectangle

The area of rectangle is equal to

`A=45*80=3,600\ ft^(2)`

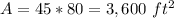
step 2

Find the area of semicircle

The area of semicircle is equal to

`A=(1)/(2)\pi r^(2)`

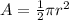
we have

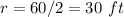`r=60/2=30\ ft` -----> the radius is half the diameter

substitute

`A=(1)/(2)(3.14)(30)^(2)`

`A=1,413\ ft^(2)`

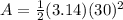
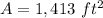
step 3

Find the total area of grass

`3,600\ ft^(2)-1,413\ ft^(2)=2,187\ ft^(2)`