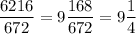Question

How do I calculate following equations?


`((21)/(22) + (4)/(15) ) + 1 (11)/(15) \\ \\ ( (3)/(14) + (9)/(32) ) / (3)/(56)`
​

Answer 1

These aren't equations, just expressions you have to evaluate.

In order to add two fractions that have different denominators, you need to express those fractions in terms of a common denominator by finding the LCM of all the denominators involved.

###

For the first expression,

`\mathrm{lcm}(22,15)=330`

because 22 = 2 * 11 and 15 = 3 * 5 share no common divisors, so the LCM would be their product.

Mixed fractions should be rewritten as improper ones:

`1(11)/(15)=(15)/(15)+(11)/(15)=(15+11)/(15)=(26)/(15)`

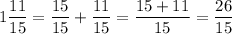
Now rewrite everything in terms of the common denominator:

`(21)/(22)=(21\cdot15)/(22\cdot15)=(315)/(330)`

`\frac4{15}=(4\cdot22)/(15\cdot22)=(88)/(330)`

`(26)/(15)=(26\cdot22)/(15\cdot22)=(572)/(330)`

`\implies\left((21)/(22)+\frac4{15}\right)+1(11)/(15)=(315)/(330)+(88)/(330)+(572)/(330)=(975)/(330)`

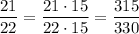
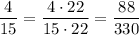
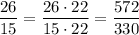
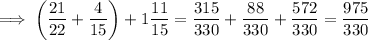
and we can rewrite this as a mixed fraction, noting that 975 = 2 * 330 + 315:

`(975)/(330)=(2\cdot330+315)/(330)=2(315)/(330)=2(21)/(22)`

###

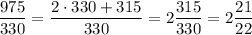
For the second expression,

`\mathrm{lcm}(14,32)=224`

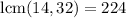
because 14 * 32 = 448, but 14 = 2 * 7 and 32 = 2^5 already share one common factor of 2 that we can factor out from 448.

Then

`\frac3{14}=(3\cdot16)/(14\cdot16)=(48)/(224)`

`\frac9{32}=(9\cdot7)/(32\cdot7)=(63)/(224)`

`\implies\frac3{14}+\frac9{32}=(48+63)/(224)=(111)/(224)`

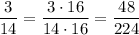
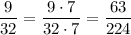
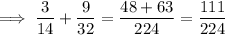
Dividing by a fraction is the same as multiply by the reciprocal of the fraction by which you're dividing. In other words,

`(111)/(224)/\frac3{56}=(111)/(224)\cdot\frac{56}3=(111\cdot56)/(224\cdot3)=(6216)/(672)`

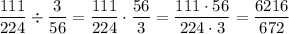
Noticing that 6216 = 9 * 672 + 168, we end up with

`(6216)/(672)=9(168)/(672)=9\frac14`