Question

Find the point, M, that divides segment AB into a ratio of 2:3 if A is at (0, 15) and B is at (20, 0).

Answer 1

What is segment ab? is there a picture that is supposed to go with it?

Answer 2

Answer: The required co-ordinates of point M are (8, 9).

Step-by-step explanation: Given that the point M divides segment AB into a ratio of 2 : 3, where A is at (0, 15) and B is at (20, 0).

We are to find the co-ordinates of point M.

We know that

the co-ordinates of a point that divides the line segment joining the points (a, b) and (c, d) are given by

`\left((mc+na)/(m+n),(md+nb)/(m+n)\right).`

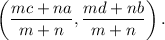
For the given division, (a, b) = (0, 15), (c, d) = (20, 0) and m : n = 2 : 3.

Therefore, the co-ordinates of point M are given by

`\left((2*20+3*0)/(2+3),(2*0+3*15)/(2+3)\right)\\\\\\=\left((40)/(5),(45)/(5)\right)\\\\\\=\left(8,9).`

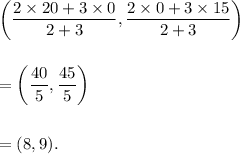
Thus, the required co-ordinates of point M are (8, 9).