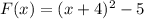Answer:
D.
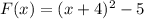
Explanation:
The parent function is
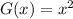 .
.
This function has its vertex at the origin (0,0).
When this function is shifted down 5 units and to the left 4 units, then its new vertex will be at (-4,-5)
The vertex form of the equation is given by;
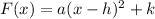 where (h,k)=(-4,-5) is the vertex and a=1 because of the parent function.
where (h,k)=(-4,-5) is the vertex and a=1 because of the parent function.
Hence its equation is