Answer:
A. The graphs of two of the functions have a minimum point.
Explanation:
Option A is false, because the only function that has a minimum point is
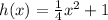
Option B is true because all the functions are of the form;

The equation of axis of symmetry of equations in this form is x=0.
Option C is also true because,
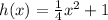 is a minimum graph and its y-intercept is 1. This graph will hang above the x-axis.
is a minimum graph and its y-intercept is 1. This graph will hang above the x-axis.
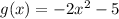 is a maximum graph whose y-intercept is -5.
is a maximum graph whose y-intercept is -5.
This graph also hangs below the x-axis.
Option D is also true. The y-intercepts are 6,-5, and 1