Question

The volume of a prism is the product of its height and area of its base, V = Bh. A rectangular prism has a volume of 16y4 + 16y3 + 48y2 cubic units. Which could be the base area and height of the prism?

Answer 1

d is the answr

Explanation:

Answer 2

Expression for Base Area is 16y² and height of the prism is y² + y + 3.

Explanation:

Given: Expression for volume of a prism =
`16y^4+16y^3+48y^2\:cubic\:units`

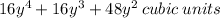
To find: Expression for the Base area and Height of the Prism.

We know that

Volume of a prism = Base Area × height

So we need to factorize given expression of volume into two factors in which 1st is for Base area and 2nd is for Height of the prism.

`Volume=16y^4+16y^3+48y^2`

Take 16y² common from each terms, we get

`Volume=16y^2(y^2+y+3)`

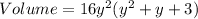
It is factorized in two factors,

So,

Base Area = 16y²

Height = y² + y + 3

Therefore, Expression for Base Area is 16y² and height of the prism is y² + y + 3.