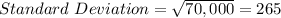Answer:
Part 1)
![[(250)^(2)+(-400)^(2)+(-250)^(2)+(350)^(2)+(100)^(2)+(-50)]=420,000](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kwcyaspgv4vx5aty4xt2ou6s5sxf74nnv4.png)
Part 2) The variance is equal to
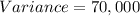
Part 3)
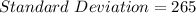
Explanation:
step 1
Find the mean of the areas
we have
![[2,400,1,750,1,900,2,500,2,250,2,100]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/27vtjj38q216f3lbz862o0drxzene2e7mw.png)
To find the mean sum all the values and divide by the number of values
The number of values is 6
so
![[2,400+1,750+1,900+2,500+2,250+2,100]/6=2.150](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yrn2gaj0obx8k8ncdotxpa5srtl32ya4m8.png)
The Mean is

step 2
For each number subtract the Mean
![[(2,400-2,150),(1,750-2,150),(1,900-2,150),(2,500-2,150),(2,250-2,150),(2,100-2,150)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1jipglevj22tgcvgl2jl27238czb17cs9k.png)
![[(250),(-400),(-250),(350),(100),(-50)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sca3t7cyd3q7l2l3nutd9fgcxlsp7ukjhe.png)
step 3
Find the Variance
To calculate the Variance, take each difference, square it, and then average the result
![[(250)^(2)+(-400)^(2)+(-250)^(2)+(350)^(2)+(100)^(2)+(-50)]=420,000](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kwcyaspgv4vx5aty4xt2ou6s5sxf74nnv4.png)
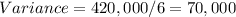
step 4
Find the standard deviation
The Standard Deviation is just the square root of Variance
so