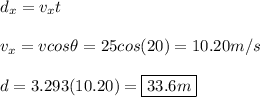Hi there!
Part C.
We can begin by solving for Part C first, which will allow us to do part B next.
Use the kinematic equation:
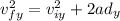
At the top of the trajectory, the final VERTICAL velocity is 0 m/s, so:
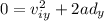
Solve for the initial vertical velocity by finding the vertical component of the given velocity:
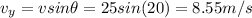
Plug in the acceleration due to gravity:
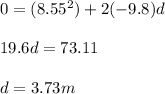
Add this to the initial height to get the total max height:
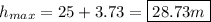
Part B.
We must solve for the times taken for the pumpkin to reach its max height and to fall down.
The time taken to reach the max height can be solved by:
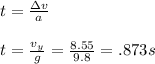
Now, solve for the time to fall from the max height solved above using the rearranged kinematic equation:
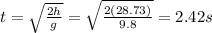
Add the times:
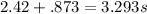
Now, using the distance/speed/time equation: