Answer:
She applied the exponent -2 to 4(-2) instead of applying the exponent to just -2
Explanation:
we have the expression
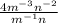
Simplify
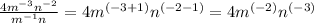
Substitute the values of m and n in the expression
For
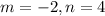
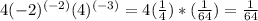
She applied the exponent -2 to 4(-2) instead of applying the exponent to just -2