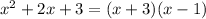Question

Students were asked to write a trinomial that could not be factored using integers. which students followed the given directions.

pat x2 + 3x- 10
sam x2+x-12
mel x2+2x-1
lee x2+2x-3​

Answer 1

Mel followed the right direction.

Step-by-step explanation

Pat's trinomial is;

`{x}^(2) + 3x - 10`

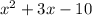
There are factors of -10 that sums up to 3.

`5 + - 2 = 3`

Hence this trinomial could be factored into (x-2)(x+5)

Sam's trinomial:

`{x}^(2) + x - 12`

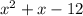
There are factors of -12 that sums up to 1.

4+-3=1

`{x}^(2) + x - 12 = (x + 4)(x - 3)`

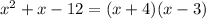
Mel's trinomial:

`{x}^(2) + 2x - 1`

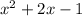
There are no factors of -1 that sums to 2.

This trinomial cannot be factored.

Lee's trinomial:

`{x}^(2) + 2x - 3`

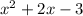
There are factors of -3 that sums up to 2

3+-1=2

`{x}^(2) + 2x + 3 = (x + 3)(x - 1)`